Phyics Informed Neural Networks (PINNs)
Phyics Informed Neural Networks はその名の通り、物理学的な情報に基づいて学習させる (Artificial) Neural Network (NN) のこと。 まあどちらかといえば equation of motions と boundary conditions を教師にするという意味で、微分方程式の解を NN で近似する手法といった方が正確。 (データと運動方程式からモデルのパラメーターを求めるなどの逆問題も含まれる。) おそらく、 M. Raissi らの Physics Informed Deep Learning (Part I): Data-driven Solutions of Nonlinear Partial Differential Equations あたりが出発点で、 automatic differentiation (AD) をうまいこと使って損失関数に微分方程式を埋め込んでいるところが epoch making なのだと思う。
学習後の NN そのものが近似解となるので、入力と出力の次元がそのまま微分方程式の座標と変数の次元になる。 なので、どの程度よく近似できるかはさておき、高次元、連立系でも拡張が容易。 原著論文で Burgers 方程式の例をやっているように、非線形系でも対応できる。
いろいろ参考ページを載せる。
- Physics-informed neural networks - Wikipedia 英語版 Wikipedia にはすでに記事がある。
- ディープラーニングで微分方程式を解く話 - Qiita 日本語でかなり早い段階でPINNsを紹介していた気がする Qiita の記事。
- 深層学習を用いた数値シミュレーション | ALBERT Official Blog ITベンチャー?による Raissi 論文の日本語レビュー記事。
さて、私は物理を嗜んでいるので、多くの問題は微分方程式を解くことに帰着する。 基本的には脳死で Mathematica の NDSolve に解いてもらうのだが、 Wolfram の力を借りても PDE の解析は難しいというかめんどくさい。 PINNs は PDE をお気楽に解けるような気がするのでぜひ習得したい! Raissi はコードを github に載せているが、 Python と TensorFlow 1.0 で解読困難。 もがいた挙句、新進気鋭の言語 Julia では Flux という機械学習パッケージが使えるらしいので、これで PINNs の練習をしたいと思った。 しかし、PINNs のアイデアの核となる、損失関数に AD を使ってそのまま eom を書くということはなかなか奇抜で、どうにも勾配がちゃんと計算できなかったりする。 その経緯のメモ。
- The Fast Track to Julia Julia のチートシート
- Home · Flux Flux の Documentation
自明なフィッティング(回帰問題)
まず、自明な問題として次を考える。 $$ y(x) = \sin(x) $$ この $y(x)$ を NN で近似する。コードは次のようになる。 まず Flux で中間層2、ニューロン数32の NN モデルを構築する。
using Flux
y = Chain(
x->fill(x,1,1),
Dense(1,32,σ),
Dense(32,32,σ),
Dense(32,1),
x->x|>sum
)
ps = Flux.params(y)Chain の中に関数を連ねることで一連のネットワークを構築できる。 Dense が Affine layer で最後の引数に activation function を入れる。 (σ は Flux で定義された sigmoid で Jupyter notebook では \sigma のあと Tab を押せば入力できる。) Flux では関数の引数か、 Params(W) などした変数 W が AD の対象になる。 Flux.params(y) は NN の重みパラメータなどを全てまとめて Params 型で返してくれる。
損失関数 (loss) は $y(x)$ と $\sin(x)$ の squared error とする。
function loss(x)
return (y(x) - sin(x))^2
endoptimizer に ADAM を指定して $x=1$ の一点について勾配を計算して学習させる。
opt = ADAM()
x = 1.0
@info loss(x)
gs = gradient(ps) do
training_loss = loss(x)
return training_loss
end
Flux.update!(opt, ps, gs)
@info loss(x)Julia で特徴的なこの do 構文 は do-end の中の関数を gradient の第一引数にする。 なので gradient(loss, ps) のようなものが評価される。 たぶん、第二変数が Params だと gradient は Grads を返す。 gs.grads をみると IdDict が入っていて、これに従って Flux.update! でモデルのパラメーター ps を更新する。 学習前後の loss の値は初期化の乱数で違うと思うが、おそらく減っているはず。
$0\lt x \lt 2\pi$ の間の50点を等間隔にとって、学習ループを回す。(オンライン学習)
# 配列 X の各点で学習させる関数
function train_online(X)
for x in X
gs = gradient(ps) do
training_loss = loss(x)
return training_loss
end
Flux.update!(opt, ps, gs)
end
end
X = range(0,2π,length=50)
@info loss.(X)|>sum #Info: 122.22932915599992
for i in 1:5000
train_online(X)
current_loss = loss.(X)|>sum
if i%1000==0
display("step: $i; mse: $current_loss")
end
end
@info loss.(X)|>sum #Info: 0.02056086919277741関数名と()の間の . は broadcast で引数に配列を渡すと map した結果を返す。(演算子に対して使う時は . を前につける) |> は pipe で前の結果を後ろの関数に渡す。
5000回のループでかなり loss が減ったのでこれをプロットしてみる。
using Plots
plt = plot()
plot!(plt,x->y(x),xlim=(0-1.0,2π+1.0),xlabel="x",ylabel="y", label="NN", size=(450,320))
plot!(plt,sin,xlim=(0-1.0,2π+1.0), label="exact")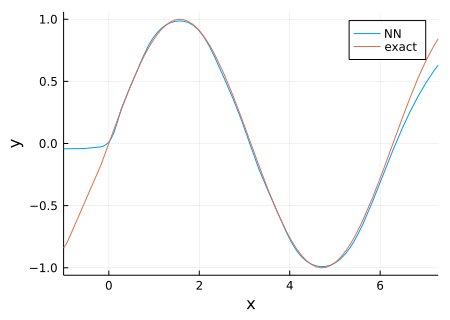
こんな結果になる。学習は $0<x<2\pi$ で行ったのでその間でのみよく近似できている。
少し非自明な問題
まだ微分方程式ではないが、問題を少し非自明にして次の非線形代数方程式を解かせることもできる。
$$ (x-a)^2 + y(x)^2 = a^2,~~~a = 3. $$もちろん解は $y(x) = \pm\sqrt{a^2 - (x-a)^2}$ となる。 答えを知っているからだが、$0 \lt x \lt 6$ しか方程式の解は実でないので、このレンジを入力として学習させる。 (モデルを複素数にすれば良かった気がする。)
Flux.update! よりもデータセットを引数にできる Flux.train! で学習をかけることにする。 Training · Flux の "Custom Training loops" によると、Flux.train! は Flux.update! を各データに対してかけているのと同じらしい。 よって、 loss としては方程式の sampling points に渡っての mean squared error を設定する。
function loss(X)
a = 3.0
mse = sum((y.(X).^2 .+ (X.-a).^2 .- a^2).^2)/length(X)
return mse
end全体のコードは次のようになる。
using Flux
y = Chain(
x->fill(x,1,1),
Dense(1,64,σ),Dense(64,64,σ),Dense(64,1),
x->x[1]
)
ps = Flux.params(y)
function loss(X)
a = 3.0
mse = sum((y.(X).^2 .+ (X.-a).^2 .- a^2).^2)/length(X)
return mse
end
opt = ADAM()
using Random
X = range(0,6,length=50)
loss(X)|>display #Info: 37.05929889911021
for i in 1:5000
Xs = Random.shuffle(X)
Flux.train!(loss, ps, Xs, opt)
current_loss = loss(Xs)
if i%1000==0
display("step: $i; mse: $current_loss")
end
end
loss(X)|>display #Info: 0.07867109363853353おそらく、 Flux.train! を使っても順番に勾配を適用していくオンライン学習であるためか、 Random.shuffle を使って入力データの順番を毎回変えた方が性能がよくなった。 次で結果をプロットする。
using Plots
plt = plot()
plot!(plt, x->sqrt(3^2-(x-3)^2), xlim=(0,6),
xlabel="x", ylabel="y", size=(450,320),
linestyle=:dash, linecolor=:red, label="exact")
plot!(plt, x->-sqrt(3^2-(x-3)^2), xlim=(0,6), linestyle=:dash, linecolor=:red, label=nothing)
plot!(plt, x->y(x), xlim=(-0.5,6.2), label="NN", linecolor=:blue)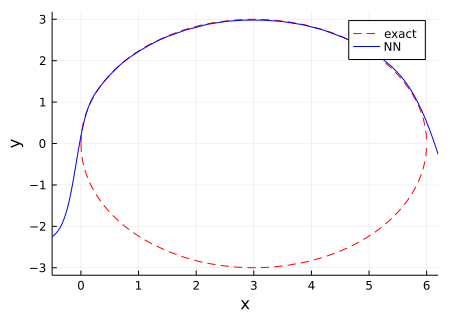
解析解の微分が発散する $x = 0, 6$ の端ではやはりあまり合っていないが、他は概ねよく近似できている。 解析解としては符号の異なる2つの解があるが、今の場合、どちらに落ち着くかはモデルの初期化と学習過程に寄っているのでわからない。 必要なら、損失関数に relu(-y(x)) など足せば、負符号の結果は不利になるので、常に正符号の解に収束させることもできる。
微分方程式にチャレンジ!
自動微分 (AD)
直感的には前述の例を微分方程式(と境界条件)に置き換えれば PINNs ができそうだが、 その前に自動微分 automatic differentiation (AD) が Flux で正しく動作するか確かめる。
using Flux
f(x) = x*exp(-x)*exp(5)
fx = Flux.gradient(f,5)
display(fx) #(-4.0,)
fxx = Flux.gradient(x->Flux.gradient(f,x)[1],5)
display(fxx) #(3.0,)$f(x) = x e^{-x+5}$ に対して
$$ f'(5) = \left.e^{-x+5}(1-x)\right|_{x=5} = -4, $$なので正しい結果が得られている。また、2階微分は
$$ f''(x) = \left. e^{-x+5}(x-2) \right|_{x=5} = 3, $$なのでこれも正しい。 他にも Flux.jacobian とか Flux.hessian とかもある。 f を NN に変えても当然微分できる。
微分を含む損失関数
問題として
$$ y'(x) = \cos(x),~~y(0) = 1, $$を考える。解析解は $y(x)=\sin(x)+1$ となる。 とりあえず次のようにモデルを作る。
using Flux
nₕ = 32
y = Chain(
x -> fill(x,1,1),
Dense(1,nₕ,tanh),Dense(nₕ,nₕ,tanh),Dense(nₕ,1),
x -> x[1])
yₓ(x) = Flux.gradient(f,x)[1]
ps = Flux.params(y)
opt = ADAM()loss として方程式と境界条件それぞれの自乗誤差の和をとる。
function loss(X)
mse_eq = sum((yₓ.(x).-cos.(x)).^2)/length(X)
mse_bc = (y(0.0)-1.0)^2
return mse_eq + mse_bc
end
ps = Flux.params(y)
opt = ADAM()
x = 1.0
@info loss(x)
Flux.train!(loss, ps, x, opt) # error
@info loss(x)Mutating arrays is not supported -- called setindex!(::Matrix{Float64}, _...)
なんかエラーが出る。
Derivative in loss function error · Issue #1464 · FluxML/Flux.jl · GitHub
ここによると setindex がよくないらしいので y(x) と yₓ(x) の最後を sum に変えてみる。
using Flux
nₕ = 32
y = Chain(
x -> fill(x,1,1),
Dense(1,nₕ,σ),Dense(nₕ,nₕ,σ),Dense(nₕ,1),
x -> x|>sum)
yₓ(x) = Flux.gradient(y,x)|>sum
ps = Flux.params(y)
opt = ADAM()
function loss(X)
mse_eq = sum((yₓ.(x).-cos.(x)).^2)/length(X)
mse_bc = (y(0.0)-1.0)^2
return mse_eq + mse_bc
end
x = 1.0
@info loss(x) #Info: 1.1777353263784807
Flux.train!(loss, ps, x, opt)
@info loss(x) #Info: 1.0859800649269835loss が減っている。学習ループを回してみる。
X = range(0,2π,length=50)
display(loss(X)) # 0.8886441292820905
using Random
loss_vals = []
for i in 1:500
Xs = Random.shuffle(X)
Flux.train!(loss, ps, Xs, opt)
current_loss = loss(Xs)
append!(loss_vals, current_loss)
if i%100==0
display("step: $i; mse: $current_loss")
end
end
display(loss(X)) # 0.0002647979270197581結果をプロットする。
using Plots
X = range(-π/2,2π+π/2,length=75)
Y_NN = y.(X)
Y0 = map(x->sin(x)+1.0,X)
plt = plot()
plot!(plt, X, Y_NN, label="NN", xlabel="x", ylabel="y", size=(450,280))
plot!(plt, X, Y0, label="exact")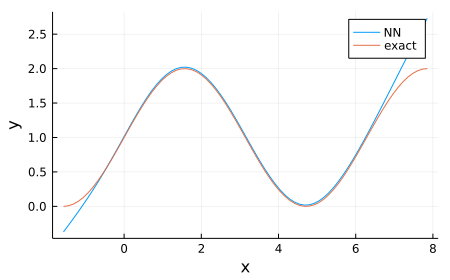
若干の誤差が残るが、解析解 $y(x) = \sin(x) + 1$ を近似できた!
loss_vals に損失関数の推移を記録しておいたのでプロットしてみる。
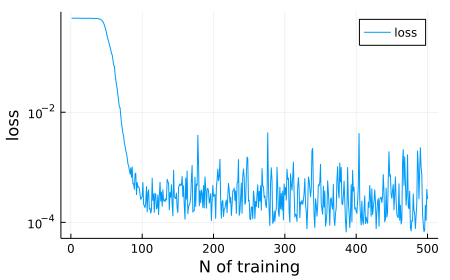
$N=100$ ぐらいでほぼ学習は頭打ちになっている。
減衰振動の問題
別の問題として次の方程式を解かせる。
$$ y''(x) + y'(x) + y(x) = 0,~~y(0)=1,~~y'(0)=-\frac{1}{2}. $$解析解は $y(x) = e^{-x/2} \cos(\sqrt{3} x /2)$ の減衰振動である。
using Flux
y = Chain(
x -> fill(x,1,1),
Dense(1,64,tanh),Dense(64,64,tanh),Dense(64,1),
x -> sum(x))
yₓ(x) = Flux.gradient(y,x)|>sum
yₓₓ(x) = Flux.hessian(y,x)|>sum
ps = Flux.params(y)
opt = ADAM()
function loss(X)
mse_eq = sum((yₓₓ.(X) .+ yₓ.(X) .+ y.(X)).^2)/length(X)
mse_bc1 = (y(0.0) - 1.0)^2
mse_bc2 = (yₓ(0.0) + 1/2)^2
return mse_eq + mse_bc1 + mse_bc2
end
(y(1.0), yₓ(1.0), yₓₓ(1.0))|>display
X = range(0,15,length=50)
loss(X)|>display # 1.466832866649817
using Random
loss_vals = []
for i in 1:500
Xs = shuffle(X)
Flux.train!(loss, ps, Xs, opt)
current_loss = loss(Xs)
append!(loss_vals, current_loss)
if i%100==0
display("step: $i; mse: $current_loss")
end
end
loss(X)|>display # 0.0004307155119744171最初の微分値評価と学習には結構時間がかかる。結果は次のよう。
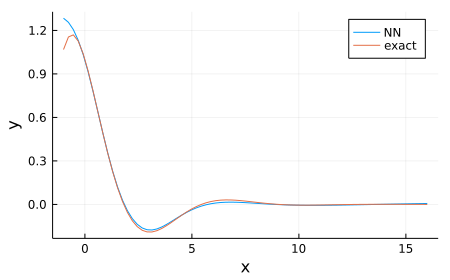

解析解に収束しきっていないが、近い形になっている。(学習点は $0\lt x \lt 15$)
問題
setindex が使えないと一次元問題にしか対応できない。 例えば次の Burger's equation
$$ \begin{gathered} u_t + u u_x - (0.01/\pi) u_{xx} = 0,~~-1 \lt x\lt 1,~~0\lt t\lt 1,\\ u(t=0,x)=-\sin(\pi x),~~u(t,-1)=u(t,1)=0, \end{gathered} $$を考えようとすると、モデルは
using Flux
u = Chain(
Dense(2,64,tanh),Dense(64,64,tanh),Dense(64,1),
x -> sum(x))
uₜ(xs) = sum(Flux.gradient(u, xs))[1]
uₓ(xs) = sum(Flux.gradient(u, xs))[2]
uₓₓ(xs) = sum(Flux.diaghessian(u,xs))[2]という感じになるが、ここで [2] とかを使わないのは無理。